YauzaCTF 2021 Lorem Ipsum Writeup
Lorem Ipsum
For this challenge we are given a single file with an excerpt of Lorem Ipsum in it. A cursory glance at the text in the file reveals nothing untoward. However, digging deeper into the bytes of the file reveals some weird stuff.
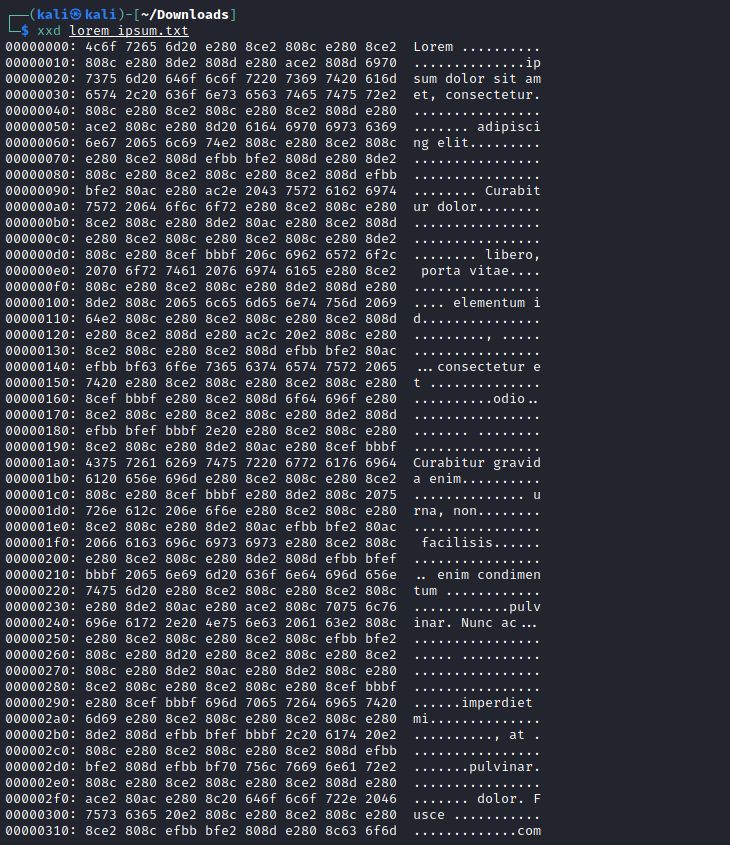
There is clearly some nonsense happening inbetween some of the words of the text. I opened the file in vim to see what it would render these characters as.

Interestingly enough, we can see here that the characters inbetween the words are a series of unicode zero-width characters. These specific characters are sometimes used to hide a secret message in normal text. They are essentially “widthless” when inserted into text and therefore do not usually visibly alter the text.
To solve this quickly, we can input the text into a zero-width steganography decoding site like the one here.
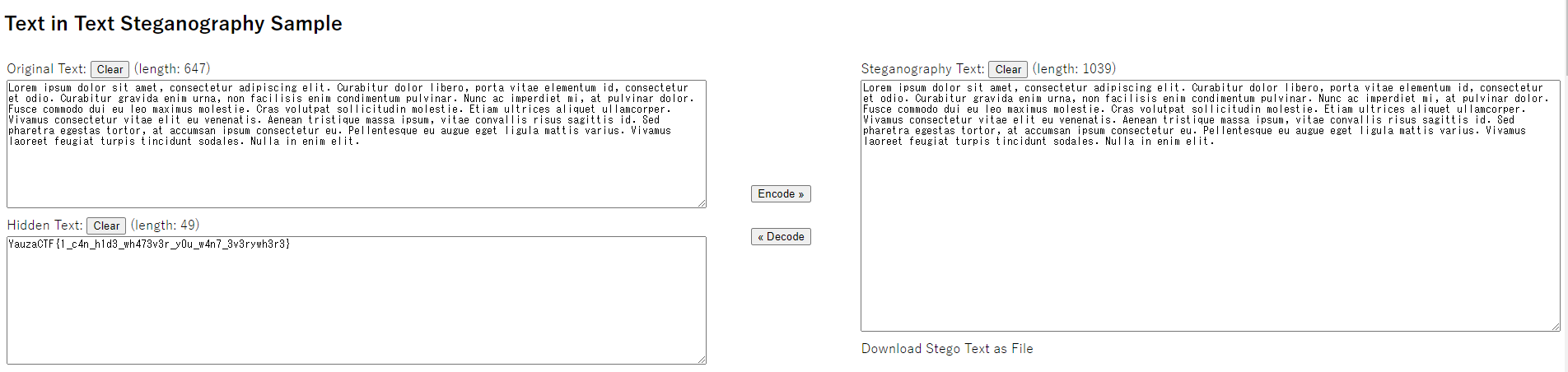
And out pops the flag. From here the challenge is complete but if you want to know more about the encoding scheme continue to read on.
Under the Hood
To create a zero-width steganographic encoding the hidden text is first converted to its binary representation (ex. a = 01100001). Next each binary “letter” (8 bits) is converted to a series of zero-width unicode characters each representing a number. For example, a simple encoding scheme would use unicode 200B (U+200B) as 0 and unicode 200C (U+200C) as 1. These unicode characters should be inserted into the public text in the spaces between words so they don’t make visible breaks in the text.
Depending on how many unique zero-width characters we use, we must change the base we are working in. So for the previous example, we are using 2 unique zero-width characters (U+200B and U+200C), meaning our result will represent a base 2 number.
Example Base 2:
a = 97 = 01100001 (base 2) ---> U+200B U+200C U+200C U+200B U+200B U+200B U+200B U+200C
b = 98 = 01100010 (base 2) ---> U+200B U+200C U+200C U+200B U+200B U+200B U+200C U+200B
If we added another zero-width character to the scheme, say U+200D, we would instead have to work in base 3.
Example Base 3:
a = 97 = 01100001 = 00010121 (base 3) ---> U+200B U+200B U+200B U+200C U+200B U+200C U+200D U+200C
b = 98 = 01100010 = 00010122 (base 3) ---> U+200B U+200B U+200B U+200C U+200B U+200C U+200D U+200D
This challenge has an ecoding that is a bit more complex but still easy enough to understand. We have the following characters hidden throughout the text
- U+200C
- U+200D
- U+202C
- U+FFEF
Here we have 4 unicode characters so we need to think in base 4 instead of base 2 or 3. To ease the process, let’s assume that the values follow an increasing order, here are the base 4 values for each zero-width character:
- U+200C = 0
- U+200D = 1
- U+202C = 2
- U+FFEF = 3
So to encode a character with this scheme we convert its decimal value to base 4 then swap in the appropriate zero-width characters.
Example:
a = 97 (base 10) = 1201 (base 4) ---> U+200D U+202C U+200C U+200D
b = 98 (base 10) = 1202 (base 4) ---> U+200D U+202C U+200C U+202C
Leading zeroes should be added in to make sure everything is uniform. For decoding purposes, they can be ignored. But in general all encoded characters should end up being the same length.
Speaking of decoding, let’s use this new knowledge to decode the hidden text. Note: while this is easy to do by hand, we can save all that time by using a decoding site like the one here

To start we need to know the general size of “blocks” of unicode. In this example it’s pretty easy to see from the first set of zero-width characters that the “block” size is 8. So 8 unicode characters are equivalent to a single plaintext character. Next we can divide the text up into sets of 8 unicode characters.
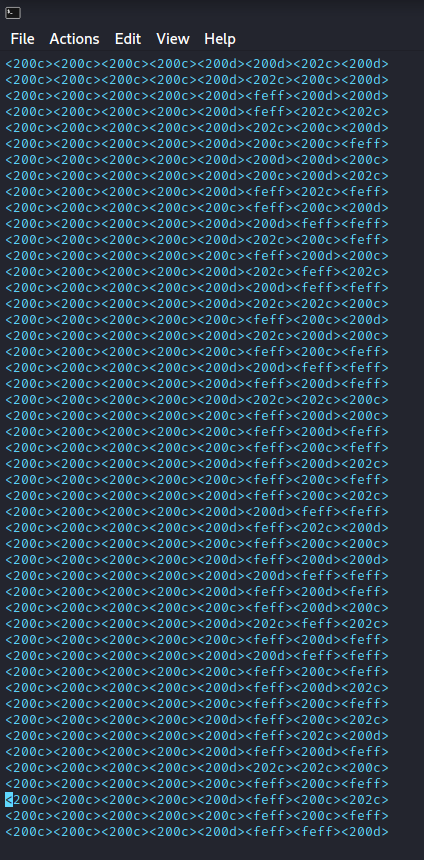
Then decoding becomes as simple as writing down the base 4 representation, converting to base 10, and finally, converting to ascii characters.
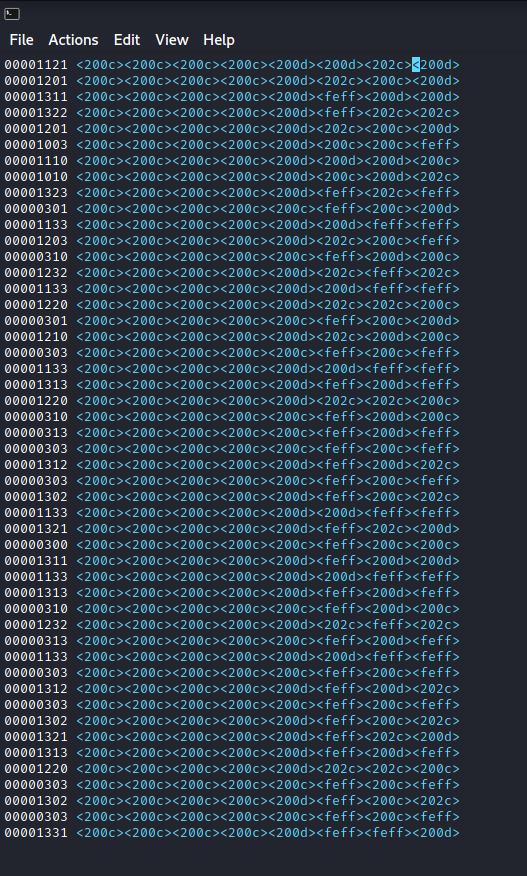
YauzaCTF{1_c4n_h1d3_wh473v3r_y0u_w4n7_3v3rywh3r3}
And that’s the long way of how to get the flag.
Lessons Learned
- Zero-Width Space Steganography (ZWSP) Encoding and Decoding
- Creating a Simple ZWSP Encoding Scheme