UMDCTF 2022 Writeup
Forensics
Renzik’s Case
My friend deleted important documents off of my flash drive, can you help me find them?
Author: matlac
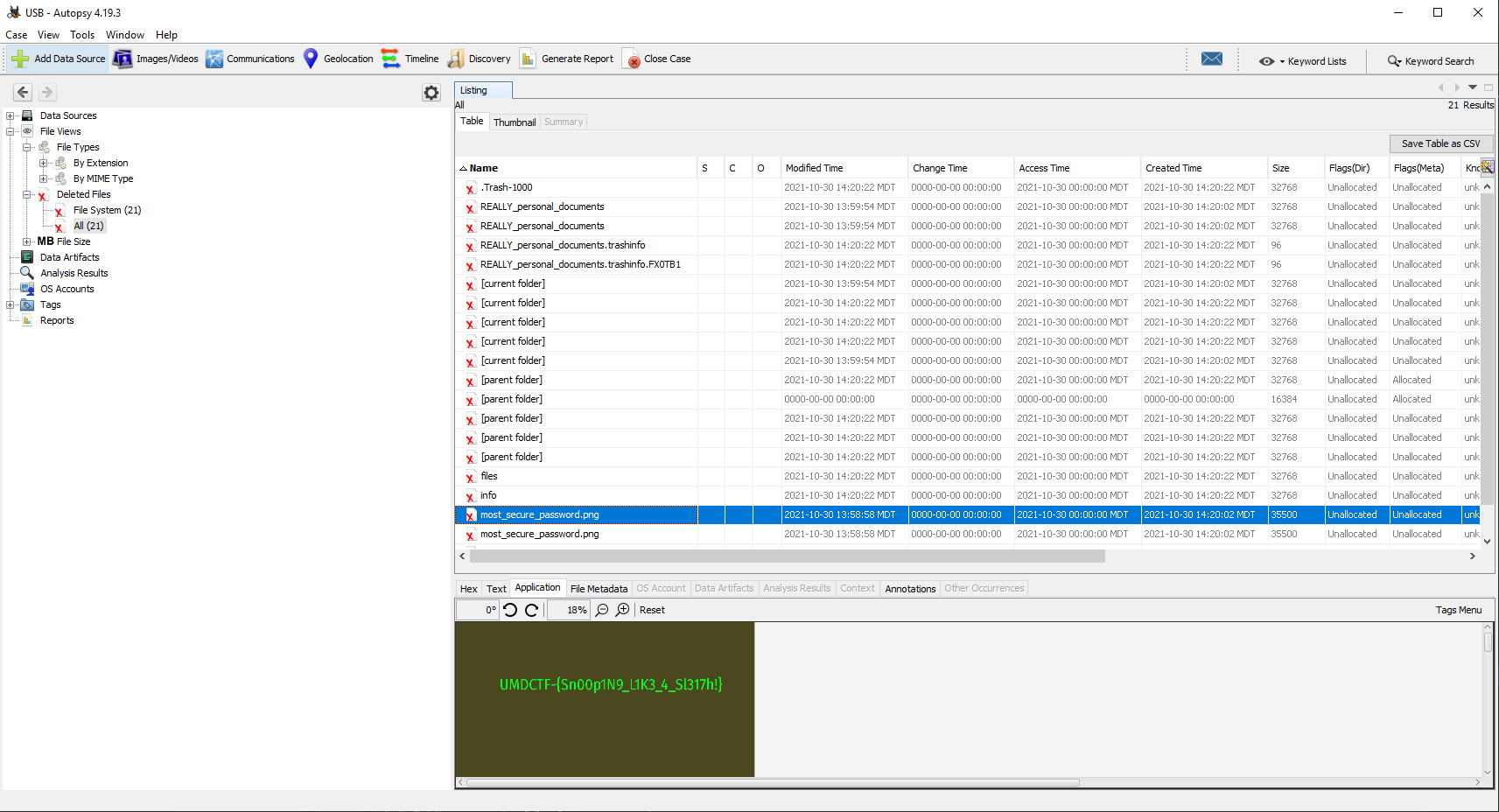
For the first forensics challenge, we are given an image of the usb detailed in the description. To begin I booted up Autopsy and imported the usb image. The usb image is very small in size so I decided to skip using any of Autopsy’s complex ingestion modules and went straight to the files.
The file we are looking for was apparently deleted so starting in
the deleted files section is the best bet. Luckily, there are only a
handful of deleted files and a few with interesting names. The most
interesting deleted file being most_secure_password.png.
Opening up the file in question in the previewer reveals the “most secure password”, the flag.
UMDCTF{Sn00p1N9_L1K3_4_Sl317h!}
Blue
Larry gave me this python script and an image. What is she trying to tell me?
Author: itsecgary
In this challenge we are given a both a PNG file and a python script. Let’s look at the image.
Well they weren’t kidding when they said this was a blue challenge. Now let’s move on to the script.
from PIL import Image
import random
#Step 1
filename = 'blue.png'
orig_image = Image.open(filename)
pixels = orig_image.load()
width, height = orig_image.size
#Step 2
with open('flag.txt', 'r') as f:
flag = f.read().strip()
# Step 3
for y in range(len(flag)):
for a in range(ord(flag[y])):
x = random.randrange(0,width-1)
c = random.randrange(0,3)
pixel = list(orig_image.getpixel((x, y)))
pixel[c] += 1
pixels[x, y] = (pixel[0], pixel[1], pixel[2])
orig_image.save('bluer.png')
In essence, the script performs a few simple tasks:
- Open a file named blue.png and uses PIL to get a list of pixels
- Open the flag and store it in a variable
- Adjust rows 0 to flag-length of pixels based on the flag
Step 3 is a bit complex so I will break it down a bit. First, the script starts a loop through the image rows, starting at row 0 and ending at row flag-length. Next, the script loops x times where x is the decimal value of the current flag character. In this loop a random pixel is taken and a random one of its RGB values is adjusted by adding 1 to it. The new RGB value is then saved back to the pixel list.
Combining this altogether, flag-length rows are adjusted to create a new image. This new image looks roughly the same as the original but contains a handful of pixels with slightly different RGB values. If we can get the RGB values of a pixel from the original image we can recreate the flag.
from PIL import Image
filename = 'bluer.png'
img = Image.open(filename)
pixels = img.getdata()
pix_list = list(pixels)
width, height = img.size
difs_by_row = list()
for y in range(height):
difference = 0
for x in range(width):
pixel = list(img.getpixel((x,y)))
difference += pixel[0] - 34
difference += pixel[1] - 86
difference += pixel[2] - 166
difs_by_row.append(difference)
result = ""
for dif in difs_by_row:
if dif != 0:
result += chr(dif)
print(result)
To solve this challenge, first we have to find a baseline RGB value. To do this we can record all the RGB value tuples in the image and the one that occurs the most is our baseline. Next, following along with the script above, we can go row-by-row through the image and find pixels that deviate from the baseline.
We can take the total difference of each pixel RGB in a row from the baseline and the result will be the corresponding character code in the flag. Finally, we can translate those decimal values back to printable characters to get the flag.
UMDCTF{L4rry_L0v3s_h3r_st3g0nogr@phy_89320}
Magic Plagueis the Wise
Did you ever hear the tragedy of Darth Plagueis The Wise? It’s written here in a magical way, but I can’t figure out how to read it. Can you help me?
Author: matlac
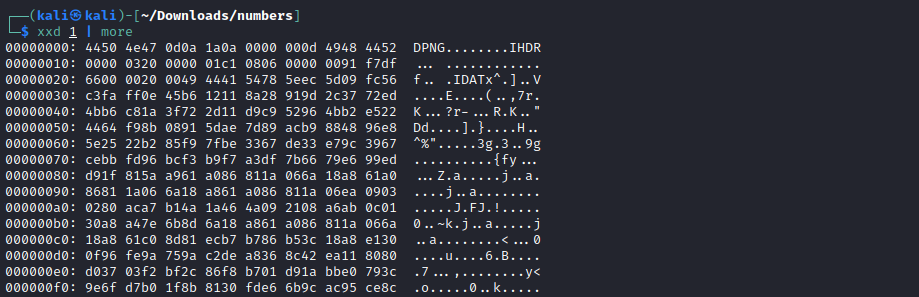
This challenge provides us with a huge number of files inside a zip. Each file is named a single number with no extension. The filename values increase, going from 1 to 4464. These files seem pretty weird so let’s look at their bytes with xxd.
The first line of the file reveals that this file could be a PNG. However, the first byte of the header is a bit off. The rest of the files are the same story, all PNG-like but the first byte of the file header is wrong.
Fixing the header seems like a good idea but doesn’t reward us much. We only get 4464 copies of the image in Figure 3.2. This led me to looking more closely at the incorrect header byte. Each byte seems to be an ascii character, maybe when they are put together they spell out something!
number = 1
res = b''
while True:
with open(str(number), "rb") as f:
f.seek(0, 0)
res += f.read(1)
if number >= 4464:
break
number += 1
print(res)
This solution script simply goes through all the files, looks at the first byte, and concatenates it to a string. Running this script results in the flag hidden between the story of Darth Plagueis the Wise.
UMDCTF{d4r7h_pl46u315_w45_m461c}
Misc
Blockchain 1 - Hashcash
Gary has an email service, but he hates spammers, so he implemented Hashcash.
Author: itsecgary
As the description suggests, to begin solving this challenge, we have to learn about Hashcash. To summarize Hashcash is
- A simple proof of work algorithm
- Used for a handful of applications like filtering spam
- Calculated by creating a header and hashing it
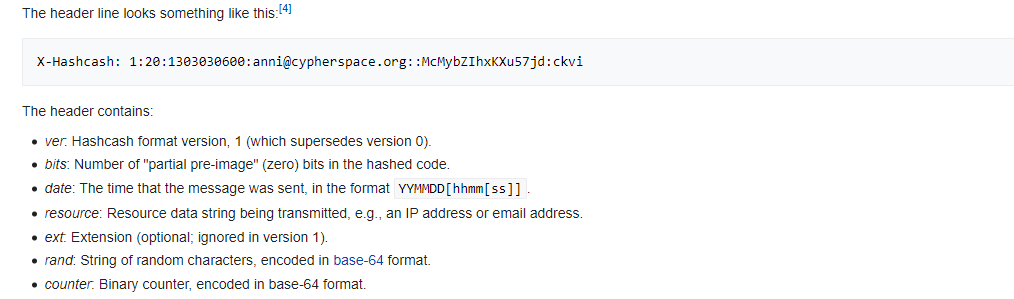
As shown in Figure 4.1, the header contains a handful of attributes to help confirm the proof of work calculation. To perform this calculation the counter part of the header is set to a random value and then the header is hashed using SHA1. If the resulting hash starts with 20-bits all with value 0, then the header is good to go. If not, then the counter is incremented and the header is hashed again. This repeats until a valid header is calculated.
Now that that’s out of the way, let’s look at the challenge.
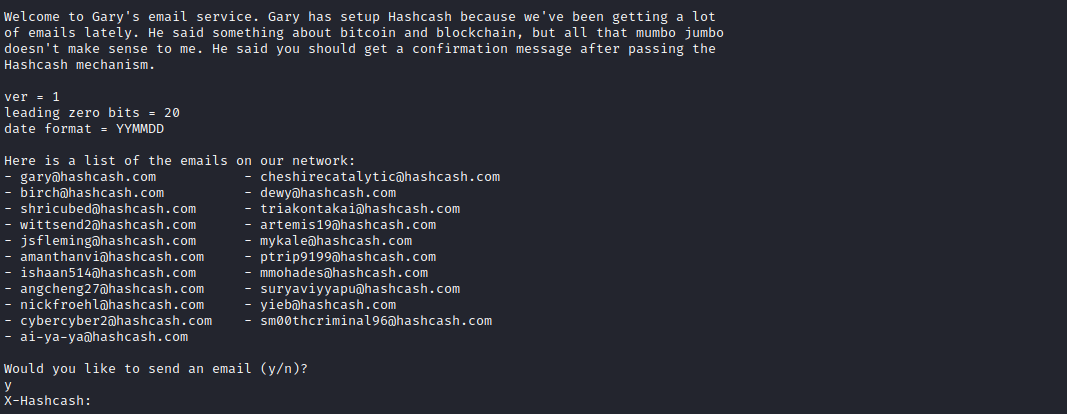
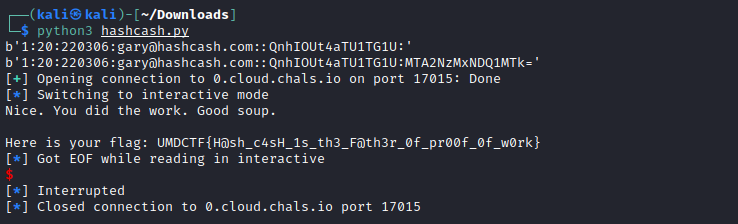
When we netcat into the challenge server, we are greeted with the message in Figure 4.2. We are given the option to send an email to someone in the list but must calculate a valid Hashcash header to send it.
import hashlib
from base64 import b64encode
from random import randint
from pwn import *
rand = b64encode(b"BxH9Kxi55LmT")
header = "1:20:220304:gary@hashcash.com::{}:".format(rand.decode()).encode()
print(header)
counter = randint(0, 125236346436)
result = ''
while True:
h1 = header + b64encode(str(counter).encode())
m = hashlib.new("sha1", h1)
hashed = m.digest()
print(hashed)
if hashed[:2] == b'\x00\x00' and hashed[2] <= 15:
result = h1
break
counter += 1
print(h1)
r = remote("0.cloud.chals.io", 17015)
r.recvuntil(b"Would you like to send an email (y/n)?")
r.sendline(b'y')
r.recvuntil(b'X-Hashcash: ')
r.sendline(result)
r.interactive()
The above solution script performs the necessary calculations and uses pwnlib to send interact with and send the header to the server. After running the script we get rewarded with the flag.
UMDCTF{H@sh_c4sH_1s_th3_F@th3r_0f_pr00f_0f_w0rk}
Crypto
MTP
One-time pad? More like multiple-time pad ;) FLAG FORMAT: Concatenate all 8 plaintext sentences together like so: “[pt1][pt2][pt3][pt4][pt5][pt6][pt7][pt8]” and take the MD5 hash of this string. Wrap the MD5 hash in the flag format to submit.
Author: itsecgary
If you know a bit about crypto, you know that using a one-time pad more than once is a big no-no. In this challenge, we see the result of that. For the challenge, we are given a script which creates ciphertexts from a one-time pad.
import random
from binascii import unhexlify, hexlify
KEY_LEN = 30
keybytes = []
for _ in range(KEY_LEN):
keybytes.append(random.randrange(0,255))
print(f'key = {bytes(keybytes)}')
key = keybytes
with open('plaintexts.txt', 'r') as f:
pts = f.read().strip().split('\n')
cts = []
for pt in pts:
ct_bytes = []
for i in range(len(pt)):
ct_bytes.append(ord(pt[i]) ^ key[i])
cts.append(bytes(ct_bytes))
print(' ')
with open('ciphertexts.txt', 'w') as f:
for ct in cts:
print(hexlify(ct).decode())
f.write(hexlify(ct).decode() + '\n')
Here the keybytes represent the pad and are used to encrypt several different plaintexts. The output ciphertexts.txt ends up looking like the following:
c909eb881127081823ecf53b383e8b6cd1a8b65e0b0c3bacef53d83f80fb cf00ec8a5635095d33bfa12a317bc2789eabf95e090c29abe81dd4339ffb c700ec851e72124b6afef52c3f37cf2bcda9f74202426fa2f54f9c3797fb cd0ebe8718365b4f2bebb6277039c469dfecf05419586fb4f658dd2997fb c341ff8b562114552ff0bb2a702cc3649ea0ff5a085f6fb0f51dd93b86f4 da13f1801321085738bf9e2e24218b7fdfb9f159190c22a1ba49d43381fb cb0df2c63f721c573ebfba21702fc36e9ea9ee50000c38a5e91ddd7ab0fb c913e796023d1c4a2befbd367032d82bdfecf55e02406fa7f548ce2997f4
To break a multi-time pad (MTP) scheme like this, we need to evaluate a few things (mainly some XOR things).

So, since key XOR key = 0, we can recover m1 XOR m2 but if we want
just m1 or m2 we have to do a bit of guessing. By guessing simple
sections and comparing our guess between ciphertexts we can slowly
solve piece together all the messages. However, this can be very
slow. Luckily, there is a simple and interactive solution to this
all on Github.
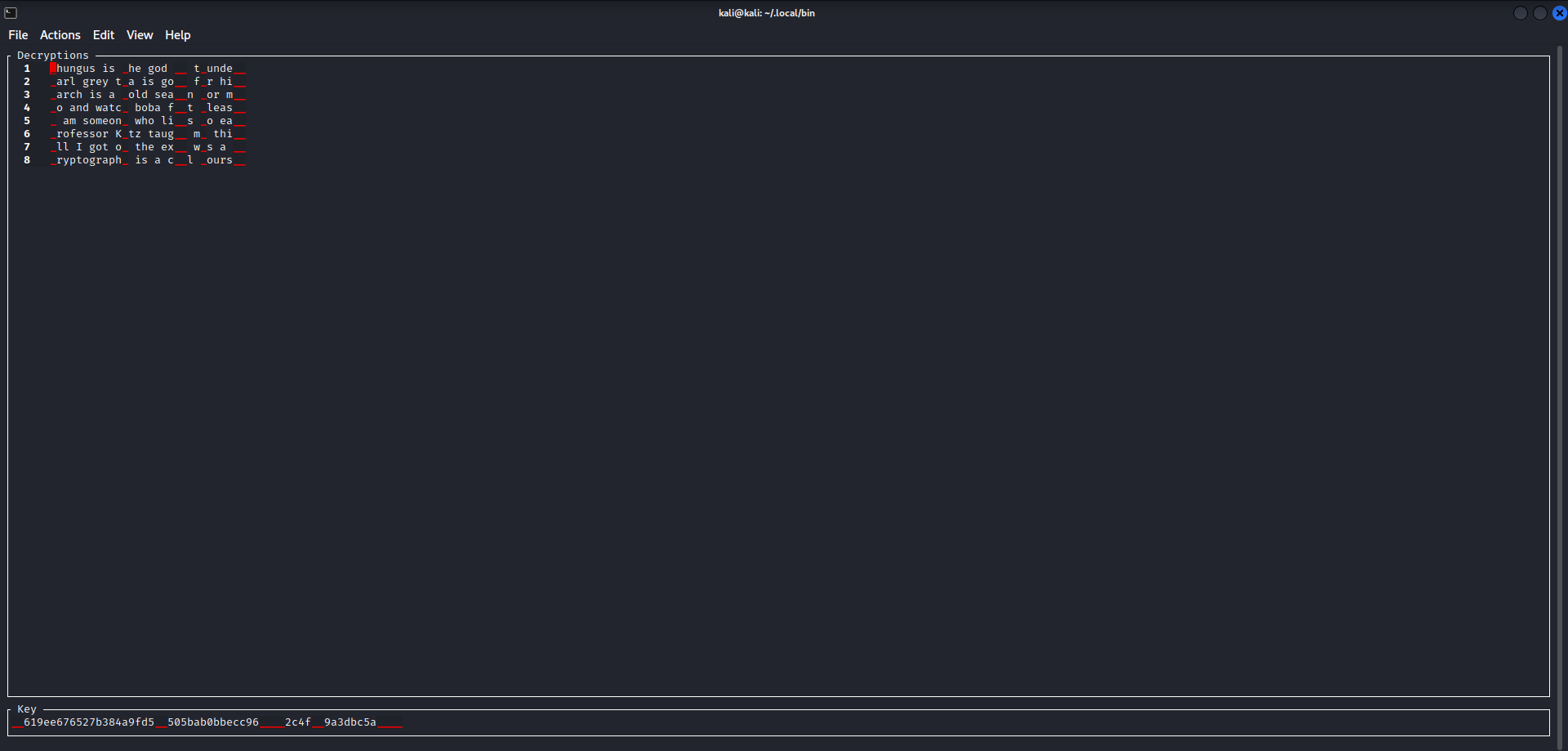
MTP Interactive partially automates and let’s us plug in value to see their results quickly. Let’s try it with out ciphertexts.
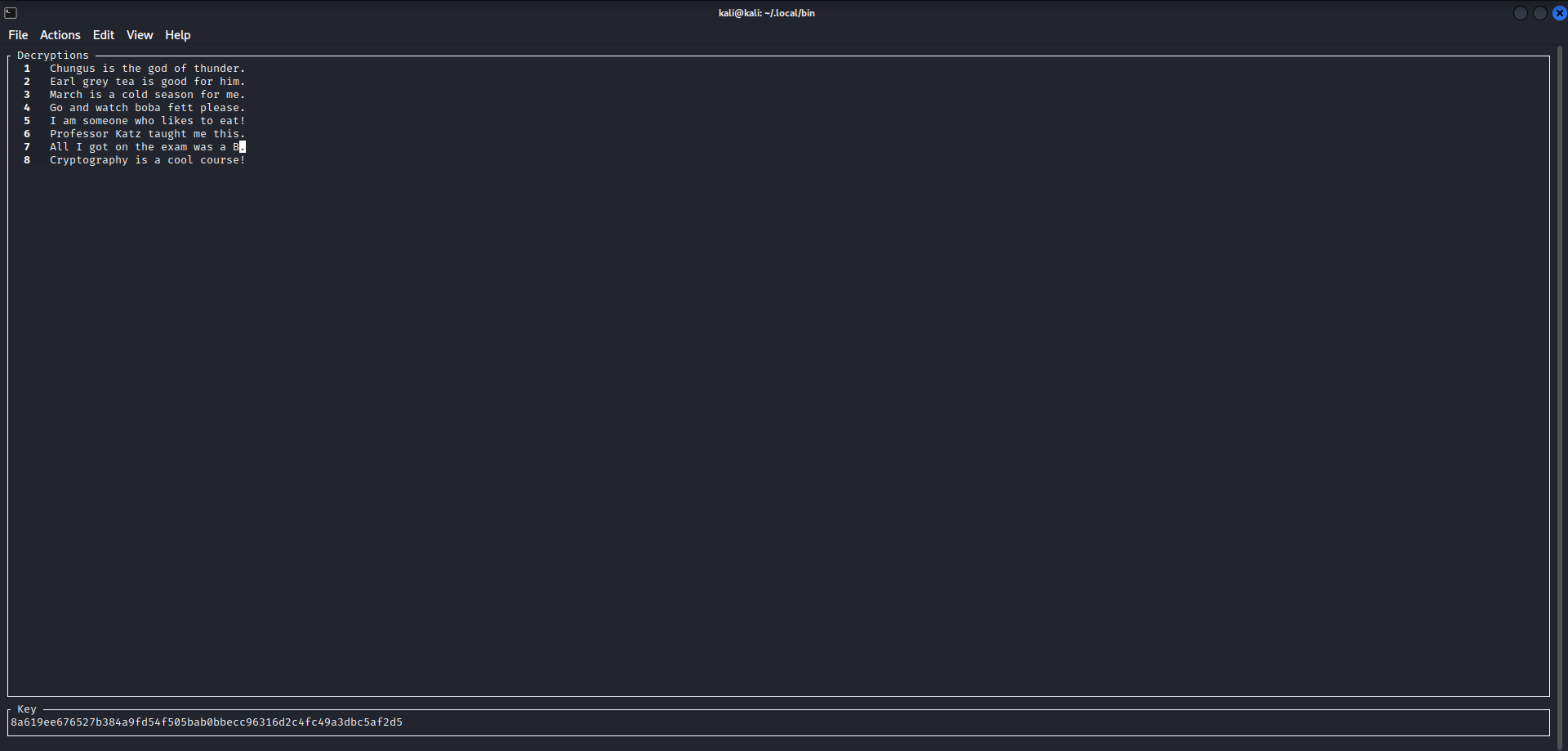
We can see that MTP decrypted a large chunk of each plaintext. Next, with a little bit of guess and check we can come up with our answer.
At this step there are two possible results but they are both easy enough to check as potential flags. Finally, we need to concatenate all the plaintexts together and hash them with md5 to create the flag.
UMDCTF{0a46e0b2b19dc21b5c15435653ffed67}
snowden
Eddy is sending encrypted messages out, but we can’t quite figure out what he is saying.
Author: itsecgary
To start this challenge, let’s netcat into the server from the description.
After an initial dialogue, the server sends us a set of RSA numbers. The interesting thing about them is that every time the n value changes but (as we are told) the underlying message stays the same. The e value also flips between a couple of low values between 21 and 29.
You might be thinking “well that isn’t very interesting” but, with a changing n value but the same plaintext and such low e values, we can recover the plaintext. The attack on this system is called a Broadcast Attack. To begin, we collect e samples of ciphertext.
from pwn import *
import json
def get_n_c_loop():
n_list = list()
c_list = list()
while True:
x = r.recvuntil(b"Want another one? (y/n) ")
r.sendline(b'y')
res = r.recvuntil(b'}').decode().replace('\'', '\"')
print("xd")
res_l = json.loads(res)
if res_l["e"] == 23:
n_list.append(res_l["n"])
c_list.append(res_l["c"])
if len(n_list) == 23:
return n_list, c_list
r = remote("0.cloud.chals.io", 30279)
r.recvuntil(b"Would you like to capture a transmission? (y/n) ")
r.sendline(b'y')
res = r.recvuntil(b'}').decode().replace('\'', '\"')
res_l = json.loads(res)
print(res_l["e"])
n_list, c_list = get_n_c_loop()
with open("n_list.txt", "w") as f:
for n in n_list:
f.write(str(n) + "\n")
with open("c_list.txt", "w") as f:
for c in c_list:
f.write(str(c) + "\n")
This simple script uses pwnlib to query the server a bunch of times until it collects 23 (you could choose any low e value that the challenge server sends) n and c values. We’ll use these values later in the actual attack.
Next let’s look at the very basics of this attack. First what we know about RSA:
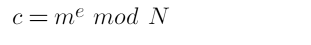
This is the simple RSA equation. Ciphertext is the result of some math being done to the plaintext. As an example let’s use e = 3 and apply what we have in the challenge:

We have 3 equations with the same m but different n and c values. From here we can apply the Chinese Remainder Theorem (CRT) which asserts the following congruencies:
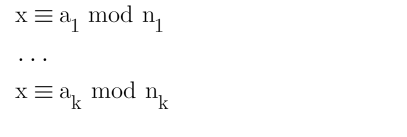
Which looks like some good math nonsense, but at a very basic level,
it turns our problem into finding some x that solves this system of
equations. We can set m^3 to some x:
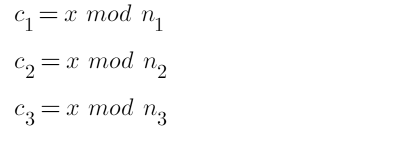
Now we only need to solve this system and find the value of x.
That bit is a bit tricky, luckily, there are a lot of
implementations online to do it for us. Either way, at the end we
have some x = m^3. From here, to recover the plaintext m, all we
need to do is take the cube root of x.
For our situation, it’s pretty much the same idea as the example. However, instead of 3 ciphertexts and a cube root we need to gather 23 ciphertexts and take the 23rd root.
import sys
import binascii
from Crypto.PublicKey import RSA
from base64 import b64decode
from functools import reduce
def chinese_remainder(n, a):
sum = 0
prod = reduce(lambda a, b: a*b, n)
for n_i, a_i in zip(n, a):
p = prod // n_i
sum += a_i * mul_inv(p, n_i) * p
return sum % prod
def mul_inv(a, b):
b0 = b
x0, x1 = 0, 1
if b == 1: return 1
while a > 1:
q = a // b
a, b = b, a%b
x0, x1 = x1 - q * x0, x0
if x1 < 0: x1 += b0
return x1
def find_invpow(x,n):
high = 1
while high ** n < x:
high *= 2
low = high//2
while low < high:
mid = (low + high) // 2
if low < mid and mid**n < x:
low = mid
elif high > mid and mid**n > x:
high = mid
else:
return mid
return mid + 1
def parseN(argv,index):
file = open(argv[index],'r')
fileInput = ''.join(file.readlines()).strip()
try:
fileInput = long(fileInput)
return fileInput
except ValueError:
from Crypto.PublicKey import RSA
return long(RSA.importKey(fileInput).__getattr__('n'))
pass
if __name__ == '__main__':
e = 23
cmd = ' '.join(sys.argv)
if '-v' in cmd or '--verbose' in cmd:
verbose = True
else:
verbose = False
n_list = list()
with open('n_list.txt', 'r') as f:
lines = f.readlines()
for line in lines:
n_list.append(int(line.strip()))
c_list = list()
with open('c_list.txt', 'r') as f:
lines = f.readlines()
for line in lines:
c_list.append(int(line.strip()))
n = n_list
a = c_list
result = (chinese_remainder(n, a))
resultHex = str(hex(find_invpow(result,23)))[2:-1]
print("")
print("~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~")
print("Decoded Hex :\n",resultHex)
print("---------------------------")
print("As Ascii :\n",binascii.unhexlify(resultHex.encode()))
print("~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~")
The solution script for this challenge is a modification of a script which can be found here. The script implements a Håstad Attack on RSA and is modified to take in our 23 ciphertexts. After running the script, we get our message from Snowden.
UMDCTF{y0u_r3ally_kn0w_y0ur_br04dc45t_4tt4ck!}
Vigenère XOR
I encrypted a big message using some kind of Vigenère Cipher. Can you figure out what it says?
Author: itsecgary
For this challenge we are faced with a Vigenère cipher. This cipher uses a repeating key and XORs it against some plaintext to provide the ciphertext. We are supplied with some code for this process.
import random
from binascii import unhexlify, hexlify
KEY_LEN = [REDACTED]
with open('plaintext.txt', 'r') as f:
pt = f.read()
with open('key.hex', 'r') as f:
key = unhexlify(f.read().strip())
ct_bytes = []
for i in range(len(pt)):
ct_bytes.append(ord(pt[i]) ^ key[i % KEY_LEN])
ct = bytes(ct_bytes)
print(hexlify(ct).decode() + '\n')
with open('ciphertext.txt', 'w') as f:
f.write(hexlify(ct).decode() + '\n')
As shown in the script, we have a unknown key of some unknown length that is XOR’d against the flag. Fairly straightforward but still a bit tricky.
Normally, this is where I find some script online to solve this for me. But by coincidence, this time I had recently been working on Cryptopals, a set of cryptography-based challenges. One of which, was to create a solver for this exact problem type.
The script is a bit long to include in text but you can find it here. Instead, I will go over the steps that it performs to decrypt the cipher.
Step 1: Finding the Key Size
To start, we have to find the key size that the cipher is using. We can do this by using a thing called Hamming Distance. Hamming Distance is simply the total difference in bits of two binary strings. For example
ab = 01100001 01100010
de = 01100100 01100101
Hamming Distance = 5
Next, we can use the hamming distance on the ciphertext to find key size. To do this, we start with a guess at the key size. Using this guessed key size, we take the first 4 (sometimes we need to do more) sets of key_size many bytes B1, B2, B3, B4, from the ciphertext. Then we compute the hamming distance between all 4 sets. We then take this result, normalize it, and record it. The key_size is then iterated and we repeat the byte comparing process.
From the set of all these normalized results, the key_size with the lowest score wins and is most-likely the actual key size.
Step 2: Split and Transpose
For the second step, we begin by splitting up the ciphertext up into key size sized chunks. Next, we “line-up” each block and separate it into columns. This means we will have a column containing the first byte of every block, a column containing the second byte of every block, etc. And that’s it for step 2!
Step 3: Single-Byte XOR Each Column
Another of the trickier steps, but by the end we will have the key to the cipher. The basic idea behind this step is to solve each column as though each byte were XOR’d with a single-byte key.
To solve a single-byte XOR cipher, we have to know a bit about character frequencies and frequency scoring. To sum up the important information
- In writing there is an average frequency at which certain letters of the alphabet appear in pieces of text
- The letter frequency ranking for English is etaoinshrdlcumwfgypbvkjxqz with e being most common
- We can use letter frequencies to score the likelihood that a ciphertext is correctly decrypted
Using these ideas we can solve a single-byte XOR cipher by bruteforce without having to go through the results manually.
So to solve single-byte XOR, we iterate through all possible single-byte values and decrypt the ciphertext with them. Then we score the ciphertexts based on how well their letter frequency matches what we expect from normal plaintext. The key with the best score wins and is probably what we are looking for.
Back to the grand scheme, we will solve each column we created in step 2 as though it were a single-byte XOR problem. When that is done we can create the Vigenère key by concatenating all the results together.
Step 4: Decrypting
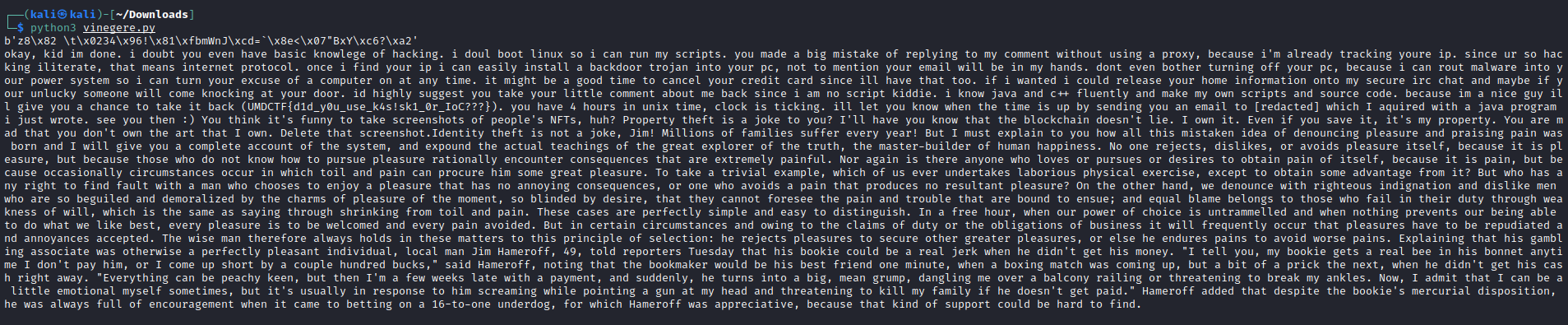
Now that we have the key, we can decrypt the original ciphertext. To do this we perform the exact same operations as we would for encrypting, except with the ciphertext in place of the plaintext. This means the ciphertext is XOR’d with the repeating key bytes and out pops the plaintext.
As here finally, we have our result, a long batch of text and the flag.
UMDCTF{d1d_y0u_use_k4s!sk1_0r_IoC???}
Conclusion
UMDCTF 2022 was a great event hosted by the team at University of Maryland and had a good difficulty range of challenges. There were some crazy good OSINT challenges as well (I didn’t solve too many of them though). The only things I would comment negatively about it were the lack of solid web challenges.
Thank you to the organizers and challenge creators, I look forward to the next year of UMDCTF.
Lessons Learned
- Searching Deleted Files in Autopsy
- Using Python PIL to Examine RGB Values
- Hiding Data in Malformed File Headers
- Blockchain Proof of Work: Hashcash Basics
- Breaking a Multi-Time Pad
- Broadcast Attacks on RSA with Low Public Exponent
- Cracking Vigenère Ciphers