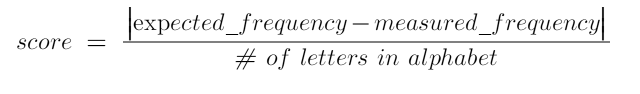Introduction

Earlier in the year I began to look at cryptography again. I realized that I don’t really understand as much as I would like to. After a little bit of searching I found the Cryptopals challenges, a series of cryptography and attack related challenges. They go over a wide range of concepts between the aforementioned attacks and implementations. The goal of these challenges is to teach people like me the various ciphers of modern cryptography and how they can fail (most commonly if implemented improperly).

As I continue to work on the challenges I plan to write a few summaries to highlight specific challenges in each set. Hopefully, I will be able to translate the nonsense I learned well enough to reteach my future self, or anyone else that happens to take on these challenges.

To begin, I would like to start with a few challenges in set 1 of Cryptopals. I will be skipping over the first couple of challenges because they don’t really need a lot of intense explaining and start off with challenge 3.

 

Challenge 3: Single Byte XOR

The hex encoded string: 1b37373331363f78151b7f2b783431333d78397828372d363c78373e783a393b3736 …

has been XOR’d against a single character. Find the key, decrypt the message. You can do this by hand. But don’t: write code to do it for you. How? Devise some method for “scoring” a piece of English plaintext. Character frequency is a good metric. Evaluate each output and choose the one with the best score.

XOR is a bitwise operation that is used in a variety of ciphers. Although a simple operation, XOR can be used in combination with a number of operations to create a fairly complex cipher. However, alone XOR is fairly weak as we will see later in this and further challenges. But first, let’s look at some simple XOR facts.

A XOR B = C

C XOR B = A

For single byte XOR, we only need to look at things in terms of single bytes. So, if we look at these equations and say that A represents some plaintext byte and B is our key-byte, then C will be the result byte of ciphertext. Equation 2 shows that the process is easily reversible if you know the value of B. In the same sense, we could figure out the value of B if we knew A, but we don’t in this case. So how do we find B? Well, we could just brute-force it but that would be a lot of results to look over to find the right one. Luckily, there is a better way, character frequency analysis.

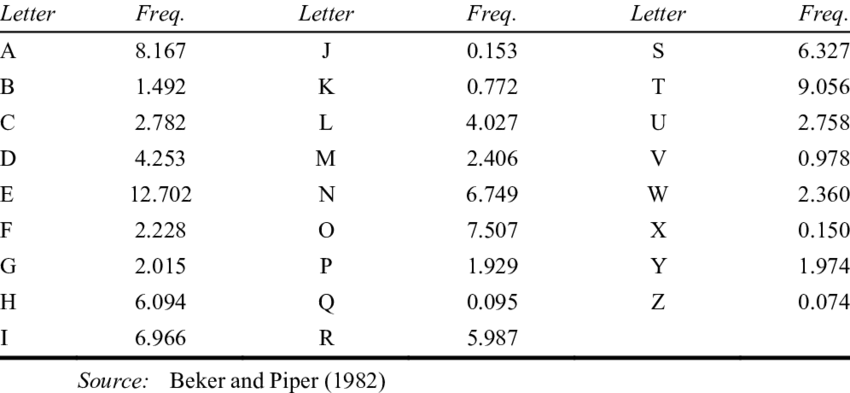
English Letter Frequency

Figure 1: English Character Frequency Table - Beker and Piper

 

For every written language there is an average frequency at which certain letters of the alphabet appear in a piece of text. Figure 1 shows the average frequency of English letters. This means that usually, things written in English contain a lot of e’s, t’s, and a’s. In fact, looking at all the previous text in this paragraph we could count and see that 13% of the letters are e’s and 9.7% are t’s.

This may seem like just a cool fact but it helps a lot for cryptanalysis, especially for simple systems like Caesar ciphers and XOR ciphers. We can use the average frequencies of letters to help guess what the decrypting key might be.

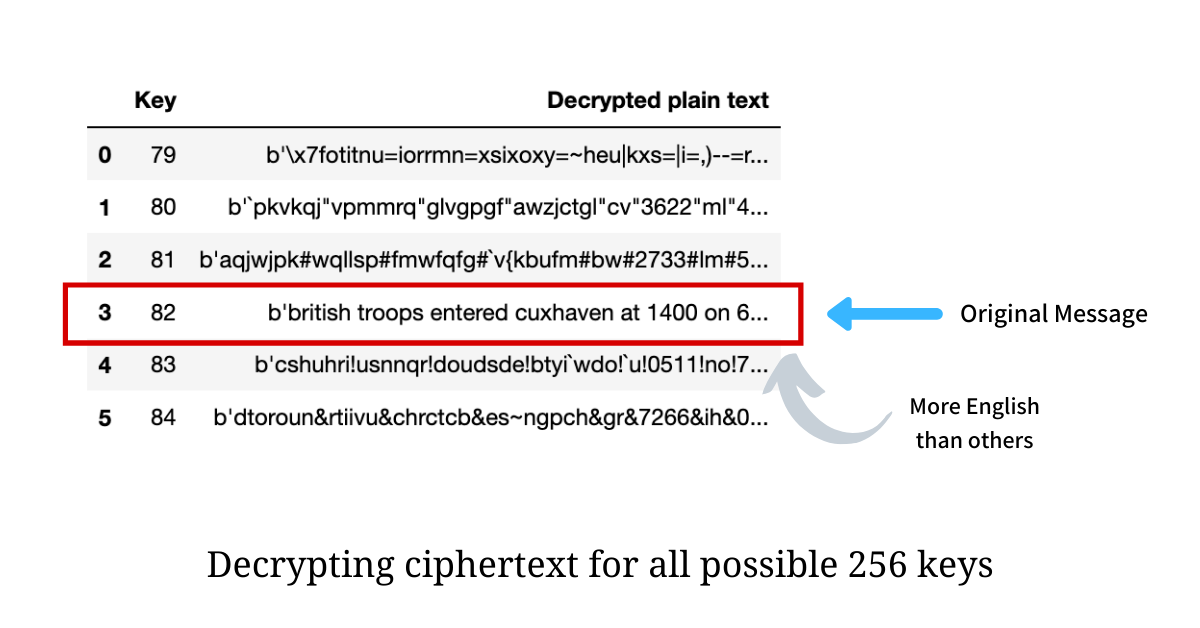
Sample Frequency Analysis

Figure 2: A Sample XOR Decoding Process Sourced from https://www.codementor.io/@arpitbhayani/deciphering-single-byte-xor-ciphertext-17mtwlzh30

 

Like Figure 2 shows, when we try to decrypt a Single Byte XOR cipher with different keys, we’ll get a variety of nonsense and clarity. Using character frequency, we can score these results based on how close they are to the average letter frequency. Frequency scoring also saves us a lot of sanity over looking through each result manually. This makes finding the correct key as simple as trying them all and finding which result has the best score. Scoring these is pretty simple using the following equation:

Scoring Equation

Applying this back to the challenge, we just need a program that does a few of things:

  1. XOR each letter in the ciphertext with a single byte (a potential key)
  2. Record the resulting plaintext and counts the characters in it
  3. Score the plaintext based on its character frequency
  4. Repeat until all possible keys have been tried
  5. Print out the message that had the best score
def single_byte_xor_solver(byte_str):
    score_list = list()
    result_list = list()
    # Loop through every potential key
    for i in range(256):
        result = b''
        for j in range(len(byte_str)):
            # XOR each ciphertext byte with the key
            result += long_to_bytes(byte_str[j] ^ i)
        result_list.append(result)
        # Count and score the resulting plaintext
        score_list.append(char_frequency_scorer(result.lower()))
    score_index = score_list.index(min(score_list))
    result = result_list[score_index]
    # Return the best score and its resulting plaintext
    return result, score_index, min(score_list)

You can find the full source code for my solution here. This small code segment performs the main loop of my solution. The script loops through all possible keys in order to find the one that the ciphertext was XOR’d with. Once all possibilities are tried, the script outputs the result with the best score, which happens to be

b”Cooking MC’s like a pound of bacon”

 

Challenge 4: Detect Single Byte XOR

One of the 60-character strings in this file has been encrypted by single-character XOR.

Find it.

Now that we know how to decrypt single byte XOR, we can also find it in a haystack of other potential ciphertexts. Using the Challenge 3 solution on each ciphertext, we can find the best score from a list of best scores in order to detect single byte XOR.

def detect_single_byte_xor(cipher_strings):
    results_list = list()
    score_list = list()
    for cipher_str in cipher_strings:
        result, key, score = single_byte_xor_solver(cipher_str)
        results_list.append(result)
        score_list.append(score)
    return results_list[score_list.index(min(score_list))]

This solution does just that and returns and decrypts the ciphertext that is most likely to be encrypted with single byte XOR. The script provides the following output:

b’Now that the party is jumping\n’

 

Challenge 5: Implement Repeating Key XOR

Here is the opening stanza of an important work of the English language:

Burning ‘em, if you ain’t quick and nimble I go crazy when I hear a cymbal Encrypt it, under the key “ICE”, using repeating-key XOR.

In repeating-key XOR, you’ll sequentially apply each byte of the key; the first byte of plaintext will be XOR’d against I, the next C, the next E, then I again for the 4th byte, and so on.

I won’t go too in-depth with this one as the concept is fairly straightforward. Basically, we need to encrypt our plaintext with a key that repeats itself. Here is a simple example to visualize this:

Key = ICE

Y E L L O W S U B M A R I N E
I C E I C E I C E I C E I C E      XOR

This system is also known as a type of Vigenere cipher and as we can see, the key will cycle until the end of the input plaintext. It can also be thought of almost like single byte XOR, except, our XOR byte changes by going through a small sequence. To implement this cipher we need to do just that, XOR each single byte with the corresponding key-byte and cycle the key as we go. Full solution code can be found here if you’re interested.

 

Challenge 6: Break repeating-key XOR

There’s a file here. It’s been base64’d after being encrypted with repeating-key XOR.

Decrypt it.

Here’s how:

  1. Let KEYSIZE be the guessed length of the key; try values from 2 to (say) 40.
  2. Write a function to compute the edit distance/Hamming distance between two strings. The Hamming distance is just the number of differing bits. The distance between:

    this is a test

    and

    wokka wokka!!!

    is 37. Make sure your code agrees before you proceed.

  3. For each KEYSIZE, take the first KEYSIZE worth of bytes, and the second KEYSIZE worth of bytes, and find the edit distance between them. Normalize this result by dividing by KEYSIZE.
  4. The KEYSIZE with the smallest normalized edit distance is probably the key. You could proceed perhaps with the smallest 2-3 KEYSIZE values. Or take 4 KEYSIZE blocks instead of 2 and average the distances.
  5. Now that you probably know the KEYSIZE: break the ciphertext into blocks of KEYSIZE length.
  6. Now transpose the blocks: make a block that is the first byte of every block, and a block that is the second byte of every block, and so on.
  7. Solve each block as if it was single-character XOR. You already have code to do this.
  8. For each block, the single-byte XOR key that produces the best looking histogram is the repeating-key XOR key byte for that block. Put them together and you have the key.

This code is going to turn out to be surprisingly useful later on. Breaking repeating-key XOR (“Vigenere”) statistically is obviously an academic exercise, a “Crypto 101” thing. But more people “know how” to break it than can actually break it, and a similar technique breaks something much more important.

Like the Crytopals web page says, this is the first fairly tricky challenge and requires a bit of work. Let’s break it into parts.

 

Part 1: Finding the Keysize

To start, we have to find the key size that the cipher is using. We can do this by using a thing called Hamming Distance. Hamming Distance is simply the total difference in bits of two binary strings. For example

ab = 01100001 01100010

de = 01100100 01100101

Hamming Distance = 5

Next, we can use the hamming distance on the ciphertext to find key size. To do this, we start with a guess at the key size. Using this guessed key size, we take the first 4 (sometimes we need to do more) sets of key_size many bytes B1, B2, B3, B4, from the ciphertext. Then we compute the hamming distance between all 4 sets. We then take this result, normalize it, and record it. The key_size is then iterated and we repeat the byte comparing process.

def find_xor_key_size(bytes_str):
    distances = list()
    key_sizes = list()
    for i in range(2, 40):
        b1 = bytes_str[:i+1]
        b2 = bytes_str[i:i*2+1]
        b3 = bytes_str[i*2:i*3+1]
        b4 = bytes_str[i*3:i*4+1]

        # Average the distances from the 4 blocks of bytes
        distances.append(
            (compute_hamming_distance(b1, b2) / i) +
            (compute_hamming_distance(b1, b3) / i) +
            (compute_hamming_distance(b1, b4) / i) +
            (compute_hamming_distance(b2, b3) / i) +
            (compute_hamming_distance(b2, b4) / i) +
            (compute_hamming_distance(b3, b4) / i) / 6
        )
        key_sizes.append(i)
    return key_sizes[distances.index(min(distances))]


def compute_hamming_distance(b1, b2):
    distance_result_str = bytes_to_long(b1) ^ bytes_to_long(b2)
    binary_rep = bin(distance_result_str)[2:]
    distance = 0
    for char in binary_rep:
        if char == '1':
            distance += 1
    return distance

From the set of all these normalized results, the key_size with the lowest score wins and is most-likely the actual key size.

 

Step 2: Split and Transpose

For the second step, we begin by splitting up the ciphertext up into key size sized chunks. Next, we “line-up” each block and separate it into columns. This means we will have a column containing the first byte of every block, a column containing the second byte of every block, etc. And that’s it for step 2!

# Break up ciphertext into key_size blocks
blocks = [bytes_str[i:i+key_size] for i in range(0, len(bytes_str), key_size)]
# Transpose key_size blocks into blocks ordered by byte
ordered_blocks = [b'']*key_size
  for i in range(len(ordered_blocks)):
      for j in range(len(blocks)):
          if i >= len(blocks[j]):
              break
          ordered_blocks[i] += blocks[j][i].to_bytes(1, 'big')

 

Step 3: Solve Single-Byte XOR For Each Column

Another of the trickier steps, but by the end we will have the key to the cipher. The basic idea behind this step is to solve each column as though each byte were XOR’d with a single-byte key.

Luckily, we went over how to solve single-byte XOR earlier so we can just copy-paste that solution into this step. Each column we solve this way will give us the corresponding byte from the key. So by the end of solving all of the columns we will have the full key. Which, in this case is

Terminator X: Bring the noise

 

Step 4: Decrypting

Now that we have the key, we can decrypt the original ciphertext. To do this we perform the exact same operations as we would for encrypting, except with the ciphertext in place of the plaintext. This means the ciphertext is XOR’d with the repeating key bytes and out pops the plaintext.

And that’s that! Really the trickiest part of solving this challenge is getting the concepts in Step 1 right. In the end, our decryption results in the following text:

b”I’m back and I’m ringin’ the bell \nA rockin’ on the mike while the fly girls yell \n …

My full solution for this challenge can be found here and will hopefully fill in some of the gaps (in terms of implementation).

 

Challenge 7: AES ECB Mode Encryption and Decryption

The Base64-encoded content in this file has been encrypted via AES-128 in ECB mode under the key

“YELLOW SUBMARINE”.

Decrypt it. You know the key, after all.

This challenge is purely to set up the next one and is a little boring. But, nonetheless, here’s an overview.

Figure 3: ECB Encryption and Decryption Diagrams

 

AES ECB is the simplest of the modes of AES and has a number of weaknesses. It only involves a key which is used within the AES mathemagic black box to encrypt the plaintext. We’ll go over the weaknesses of this scheme in later challenges, but just know that it is very deterministic over a given input and key pair.

To implement this mode, we can simply use the AES library in the language of our choice. Like every other challenge I will use Python with the pycryptodome library.

from Crypto.Cipher import AES

def ecb_decrypt(cipher_str, key):
    cipher = AES.new(key, AES.MODE_ECB)
    plaintext = cipher.decrypt(cipher_str)
    return plaintext


def ecb_encrypt(byte_str, key):
    cipher = AES.new(key, AES.MODE_ECB)
    ciphertext = cipher.encrypt(byte_str)
    return ciphertext

This library does all the hard work for us and makes our implementation very simple. Now that we have functioning encryption and decryption functions, we can decrypt the challenge file.

b”I’m back and I’m ringin’ the bell \nA rockin’ on the mike while the fly girls yell \n …

 

Challenge 8: Detect AES ECB

In this file are a bunch of hex-encoded ciphertexts.

One of them has been encrypted with ECB.

Detect it.

Remember that the problem with ECB is that it is stateless and deterministic; the same 16 byte plaintext block will always produce the same 16 byte ciphertext.

This challenge is a fair bit more interesting. To detect ECB we rely on its deterministic nature. In ECB, whenever we encrypt a specific block of plaintext under a specific key, we will always get the same ciphertext result. Therefore, if there are any repeating blocks in our plaintext we will have a similar repetition in the ciphertext.

Figure 4: Tux Original Image and Encrypted with AES ECB

 

You’ve probably seen the image in Figure 4 before that demonstrates this fact. The colours with the same pixel values in the picture have the same resulting encrypted pixel value. Therefore, the resulting image is fairly discernable.

We can use this idea to solve the challenge fairly quickly. To solve, we will go through each ciphertext and look for repeating blocks. If we find any repetitions we can probably conclude that it was encrypted with ECB. Here is a quick function to perform this task:

from binascii import unhexlify

def detect_ecb(hex_list):
    # Turn hex ciphers into byte form
    cipher_list = list()
    if isinstance(hex_list, type(list())):
        for line in hex_list:
            cipher_list.append(unhexlify(line.strip()))
    else:
        cipher_list.append(hex_list)

    ecb_cipher = None
    repeat_index = -1
    for cipher in cipher_list:
        # Divide cipher into blocks of 16
        num_blocks = len(cipher)//16
        blocks = [cipher[i*16:(i+1)*16] for i in range(num_blocks)]

        # Check for repeating blocks
        if len(set(blocks)) != num_blocks:
            ecb_cipher = cipher
    if ecb_cipher is not None:
        repeat_index = cipher_list.index(ecb_cipher)
    return repeat_index, ecb_cipher

The script returns the index and the cipher that contains a repetition. When we input the list of hex from the challenge we get the following result encoded in base64:

2IBhl0CooZt4QKijHIEKPQhkmvcNwG9P1dLWnHRM0oPi3QUva2Qdv50RsDSFQrtXCGSa9w3Ab0

 

Conclusion

Through the first set of challenges we have encountered some interesting puzzles ranging from decoding simple XOR ciphers to dipping our toes into AES. A handful of useful cryptography lessons taught in this set can also be applied to more complex systems so they are important to keep in mind. If you aren’t already, please try a hand at some of these challenges, they are surprisingly fun and technical. The next set continues on with some AES ECB as well as some other AES modes, so look forward to that.